月度归档：2月 2021

[转载]数字调制系列：如何理解IQ ？

最近在筹划写一系列关于数字 IQ 调制的短文，以帮助初学者能够更好地理解和掌握。虽然 IQ 调制技术已经非常广泛地应用于各种无线通信应用中，但是究其细节，仍有很多人存在疑惑，尤其对于初学者。作者从事测试工作多年，对 IQ 调制略有体会，整理下来分享给大家，希望对大家有所帮助。

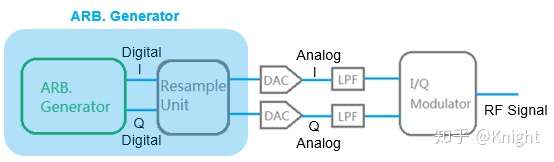
作为数字 IQ 调制系列的首篇文章，本文将主要介绍 IQ 的概念，IQ 调制的优势以及符号速率与比特率之间的关系。

1. 什么是IQ ？

回答这个问题不得不提图1所示的矢量坐标系 (复坐标系)，横轴为实部，纵轴为虚部。数字IQ调制完成了符号到矢量坐标系的映射，即每一个符号对应唯一的坐标点，该坐标点称为星座点。每一个星座点与原点构成了一个矢量，具有幅度和相位信息，在 IQ 调制中，通常默认最大的幅度为1，例如图1所示的星座点确定的矢量幅度为1、相位为45°。

矢量坐标系上任何一个点均具有实部和虚部，实部与虚部是正交的关系，在无线通信中通常将实部称为I(n-phase)分量，将虚部称为Q(uadrature)分量 。这就是术语 IQ 的由来，该矢量坐标系也可以称为 IQ 坐标系。

数字调制完成了符号到星座点的映射，每个映射点对应一个 I 分量和一个 Q 分量，二者构成一个矢量，因此数字调制又称为矢量调制。通常提到的矢量信号源就是因为具有 IQ 调制功能，才称之为矢量信号源。

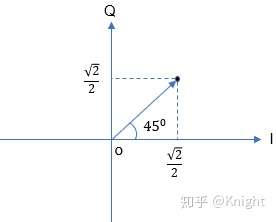
综上所述， I 和 Q 就是 IQ 坐标系上坐标点的横坐标值和纵坐标值，IQ 坐标系本质上就是复坐标系，只是在数字调制过程中称之为 IQ 坐标系，以便于实现调制。

2. 为什么引入 IQ 调制 ？

由于对数据速率要求不高，起初的无线通信基本都是采用模拟调制方式，比如AM/ FM/PM等。在相当长一段时间内，市场需求并没有大规模驱动通信技术的进步。但是随着卫星通信以及个人通信业务需求的激增，传统的模拟调制显然已经无法满足速率要求，必须要寻求支持更高数据速率的调制技术。

实践证明，IQ 调制技术可以担当此重任，我们不去深究何时引入 IQ 调制技术，而是把目光聚焦在 IQ 调制与传统的调制相比有哪些优势。

之所以采用IQ调制，主要考虑到如下优势：

(1) IQ调制可以通过提高符号速率或者采用高阶调制实现更高的数据速率，非常方便灵活，这是传统的模拟调制所远远不及的。

(2) 实现高速通信时，IQ 调制更加易于实现。IQ 调制可以非常方便地将符号映射至矢量坐标系中，从而完成数字调制；同理，在接收侧也可以非常方便地根据符号映射解调出原始数据比特流。

(3) IQ 调制具有更高地频谱利用率。如何理解呢？

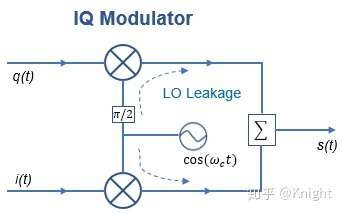
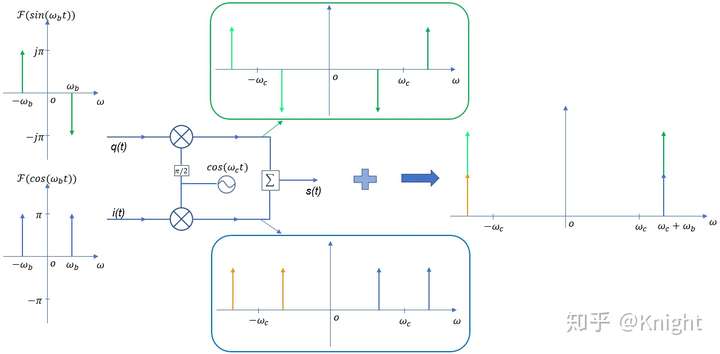
这一优势是相对于普通调制而言的，从整个 IQ 调制过程来看，I 路或者 Q 路都是普通调制， IQ 调制实际上是两个特殊普通调制的合成。图2给出了 IQ 调制器架构示意图，每一个支路上都包含一个上变频器，二者共用一个本振源，只是两路本振信号是正交的关系。上变频之前的输入信号称为基带 I 信号和基带 Q 信号，上变频且合路之后的信号通常称为射频调制信号。

为了具有普遍适用性，假设 IQ 调制的数据源为伪随机码，此时基带 I 信号和基带 Q 信号的频谱是相同的，带宽均为 B，二者均携带信息而且信息量相同。IQ 调制采用零中频架构，每一路上变频之后带宽翻倍至 2B，但是携带的信息不变。合路后，射频调制信号带宽仍然为 2B，但是相对于单路调制而言，携带的信息量翻倍了。因此，IQ调制具有更高的频率利用率！

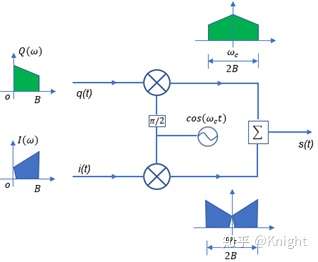
为了便于理解，下面以QPSK调制为例进一步说明。从效能上讲，QPSK调制相当于两路BPSK调制的合成，I 路调制为一路BPSK，Q 路调制为另一路BPSK。如前所述，I 路调制和 Q 路调制均为普通调制。从带宽上看，QPSK对应的射频调制信号带宽与 I 或 Q 路BPSK调制信号带宽相同；但是从数据速率上看，QPSK调制是BPSK调制的两倍。因此，IQ 调制相对于普通调制具有更高的频率利用率！

(4) IQ调制采用零中频架构，经过调制之后无需使用滤波器抑制镜频边带，设计更加灵活方便。对于其它收发机架构，比如超外差架构，由于中频不为0，经过上变频后，会存在较强的边带分量，还需要专门的镜频抑制滤波器进行滤波，这将使得设计更加复杂。

正是基于以上主要优势，IQ 调制应用才越来越广泛，几乎目前所有的无线通信中都离不开这种调制技术！

3. 数字调制中的符号速率与比特率之间有什么样的关系？

首先了解一下数字调制中“符号”的概念。前面提到，数字调制就是将0和1比特流数据按照一定的规则映射至 IQ 坐标系上，在完成映射之前需要将比特流构成符号，因此，数字调制就是将符号映射至 IQ 坐标系的过程。

每一个符号都是由比特0和/或1构成，比如：0 / 1 / 00 / 01 / 1001 / 10101……，这些都可以称为符号。一个符号至少包含一个bit信息，具体由调制方式决定。

符号映射至星座点上，意味着符号要与星座点一一对应，要实现这一点，必须要求星座点数目M与一个符号包含的比特数目N满足如下关系：

如果不满足这一点，就无法实现符号与星座点之间的映射。比如，假设存在某种调制方式，具有5个星座点，考虑两种情况：

(1) 如果一个符号包含2比特，则最多包含00 / 01 / 10 / 11四种组合，会有一个星座点用不上。既然用不上，为什么该调制方式不考虑设计为4个星座点？

(2) 如果一个符号包含3比特信息，则最多包含000 / 001 / 010 / 011 / 100 / 101 / 110 / 111八种组合，如何完全映射至5个星座点上？既然无法完全映射，那么又如何保证信息传输的完整性？

符号速率与比特率之间有什么关系呢？

符号速率 (Symbol rate) 就是单位时间内传输的符号的个数，如果一个符号包含N个比特，则对应的比特率 (Bit rate) 为符号速率的N倍。

Bit rate = Symbol rate x N

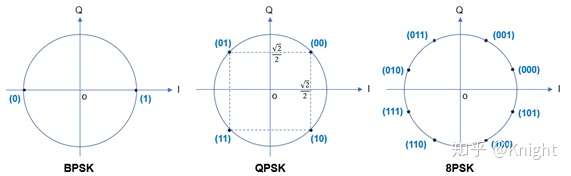
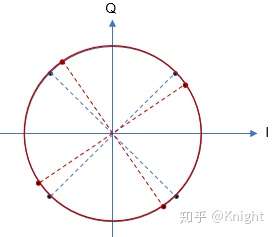
图4给出了常用的三种PSK调制方式的星座图：BPSK，QPSK和8PSK。按照上述结论，BPSK调制的比特率与符号速率相同，QPSK调制的比特率是符号速率的两倍，8PSK调制的比特率是符号速率的三倍。

小结

本文的目的就是解答初次接触数字IQ调制时可能会遇到的一些疑惑，介绍的内容都比较基础，以便于更好的理解数字IQ调制。文中着重介绍了IQ的概念、IQ调制的优势以及符号速率与比特率之间的关系，这些都是数字IQ调制的基本内容。在此基础之上，后面将陆续推出一系列的文章介绍IQ调制技术，这些都是作者多年的积累和总结，希望对大家有所帮助。

[转载]数字调制系列：IQ 调制器特性(续)

前面有知友提到 IQ 调制器载波抑制特性，并希望能够从理论上推导一下载波抑制度。关于增益不平衡及正交误差引起的边带抑制特性，在“数字调制系列：IQ调制器特性”一文中已经详细阐述。因此，本文将详细介绍一下 IQ 调制过程中载波泄露的来源及量化方式，以及从宏观的角度介绍IQ Offset、幅度不平衡及正交偏差对星座图的影响，希望对大家有所帮助。

1. IQ 调制过程中载波泄露的来源有哪些？如何量化载波泄露？要了解载波泄露的来源，需要从模拟 IQ 调制器的结构说起。IQ 调制器的关键部件是混频器，无论混频器的性能如何优异，总是存在 LO 馈通(泄露)的，而 IQ 调制采用零中频架构，LO 频率就是载波频率，故 LO 馈通是载波泄露的来源之一。

除了混频器的 LO 馈通外，载波泄露还源自哪里？模拟 IQ 信号的直流分量(DC)是另外一个来源。对于 PSK 和 QAM 数字调制方式而言，数字 IQ 信号的正、负电平可能不能完全中和，这意味着当经过 DAC 转换为模拟 IQ 信号后将存在直流分量。另外，DAC 由于自身的不理想，本身可能也会引入一定的直流分量。对于模拟 IQ 信号包含的直流，通常称为 IQ Offset。

对于 LO 馈通引起的载波泄露，这完全取决于 IQ 调制器本身，已无法改变。下面只讨论由于模拟 IQ 信号携带的直流分量引起的载波泄露。

为了量化载波泄露，并使之具有普遍适用性，假设模拟 I 和 Q 信号分别引入了一定的直流成分  和  ，二者分别是相对于各自信号振幅的相对值。

令  ，  ，则输出的射频信号为

将  和  代入上式并经过三角函数运算可得

式中  .

可见，此时  包含两部分组成：上边带和载波泄露。通常采用载波抑制度描述载波泄露多少，定义为载波泄露功率相对于主边带功率的大小。对于本例，载波抑制度为

值得一提的是，如果给出的模拟 IQ 信号的直流成分定义方式不同，所推导出的载波抑制公式会有所不同，但是推导方式类似。

2. IQ Offset、幅度不平衡及正交偏差对星座图有什么影响？上面以及之前的文章均从比较简单的单边带信号着手推导了载波抑制度、镜频抑制特性，对于复杂数字调制信号，IQ offset、幅度不平衡及正交偏差也同样会带来严重的影响。此处以 QPSK 调制为例，分别介绍这三个因素对星座图造成的影响。如果数字调制质量比较差，可以尝试从星座图上判断原因所在，为信号调试提供了依据。

(1) IQ Offset：如前所述，IQ Offset 会造成载波泄露，从频谱上看，载波非常明显。较强的载波泄露对于接收系统而言就是带内干扰，将会严重影响系统性能。从星座图上看，IQ Offset 会导致中心原点的偏移，这将恶化 EVM(Error Vector Magnitude) 。

(2) IQ 幅度不平衡：主要是指 DAC 输出的模拟 I 和 Q 信号幅度不同，以及模拟 IQ 调制器的增益不平衡。虽然对于数字调制信号而言，即使存在幅度不平衡也从频谱上观察不到镜像边带，但是确确实实会影响信号的调制质量，EVM 会恶化，星座图会被“压缩”。

(3) IQ 正交误差：主要是指模拟 IQ 调制器内部的两路 LO 信号之间的正交性不好。类似于 IQ 幅度不平衡，对于数字调制信号，即使存在正交误差，从频谱上也很难观察到异常，但依然会影响信号的调制质量，EVM 会恶化，星座图会发生旋转。

以上从星座图的角度介绍了 IQ Offset、幅度不平衡及正交误差对数字调制信号的调制质量将会有哪些影响，那么从矢量源(VSG)或者任意波信号发生器(AWG)的角度讲，是否有改善的措施呢？这将是后面要介绍的内容……

[转载]数字调制系列：IQ调制器特性

在前面关于数字调制的文章中分别介绍了 IQ 调制的基本理论及调制解调的数学解析及图解过程，阐述了常见的数字调制方式，并解释了为什么经过 IQ 调制器之后带宽会翻倍的原因。本文将着重介绍模拟 IQ 调制器的特性，为后面的 IQ 调制性能验证测试作准备。

模拟 IQ 调制器包含 Mixer，在上变频的过程中，势必会产生镜频产物。当输出无频偏信号时，即信号中心频率与调制器的 LO 信号频率相同时，相当于采用的是 Zero-IF 机制，镜频产物与信号本身不可分割，即使通过滤波器也无法滤除镜频。庆幸的是，采用IQ调制及解调器，即使存在镜频产物，依然可以恢复出原始的IQ信号。这也是为什么模拟 IQ 调制器之后不需要镜频抑制滤波器的原因。

由于这种正交架构，IQ 调制器本身是具有一定镜频抑制能力的，但是只有在输出具有一定频偏的信号时，即信号中心频率与 LO 信号频率不同时，才能体现出镜频抑制特性。下面将通过一些特殊的基带 IQ 信号进行解析分析，阐述影响镜频抑制特性的因素，及如何改善镜频抑制特性。

1. IQ 信号幅度平衡性对镜频抑制的影响。IQ信号幅度不平衡(即幅度不同)，要么是输入至调制器的 I 和 Q 信号的幅度不平衡，要么是调制器具有一定的增益不平衡 (即 I 和 Q 两路的增益不同)，这些都会影响对镜频的抑制能力。

令  ， ，则经过IQ调制输出的射频信号  为

积化和差得

当  时，射频信号中只有上边带  分量；

当  时，射频信号中只有下边带  分量；

当  时，射频信号中同时包含上边带  和下边带  两个分量。

以上通过解析方式介绍了 IQ 调制器的镜频抑制特性，其实通过图解方法也可以清晰简便地进行说明。下面考虑  的情况，图 1 给出了载波信号的傅里叶变换，这是双边带频谱，基带信号经过 IQ 调制器实现了频谱的搬移，图2分别给出了调制器两个支路上的频谱变换情况，最终经过合路器合路后，下边带分量相互抵消，只剩下上边带分量。

当  时，射频信号中同时包含上下边带，定义边带抑制比为：  dB。
如何改善镜频抑制能力呢？IQ 调制器两个支路的增益不平衡特性已经无法调整，但是可以在基带侧通过调整 I 和 Q 两路波形的幅度大小改善镜频抑制。矢量信号发生器VSG及任意波信号发生器AWG均提供了IQ Gain Imbalance调整参数，对其进行微调即可改善镜频抑制。

2. IQ 正交性对镜频抑制的影响。正交性包括两个方面：(1) 基带信号 I 和 Q 之间的正交性；(2) IQ 调制器两个 Mixer 的 LO 信号之间的正交性。如果正交性不好，当产生无频偏的数字调制信号时会带来调制和解调的误差(EVM、BER 恶化)，另一方面在产生单边带信号时，会恶化镜频抑制特性。

令  ，  ，则 IQ 调制器输出的射频信号为

积化和差得

对于  分量，令  ，  ，则取  满足如下关系：

 ， 

类似地，对于  分量，令  ，  ，则取  满足如下关系：

 ， 

以上公式代入  ，最终可得

由正交误差  造成的镜频抑制度为：  dB。

以上是从基带 I 和 Q 信号的正交性着手分析对镜频抑制特性的影响，如果基带信号理想正交 ，而 IQ 调制器两个 Mixer 的 LO 正交性不好，整个推导过程是类似的，此处不再赘述。当然，IQ 调制器的特性已经固定，只能通过调整基带信号的正交性改善镜频抑制能力。

3. IQ 调制器的载波抑制特性。IQ 调制器除了可以抑制镜频外，在数字调制过程中还可以抑制载波。理论上，只要模拟 I 和 Q 信号中没有 DC 分量，而且 IQ 调制器是理想的，那么输出的射频宽带信号中将没有载波。但是实际产生的宽带信号总是具有一定的载波泄露，来源于两部分：(1) IQ 信号中包含一定的 DC 分量；(2) IQ 调制器中 Mixer 的 LO 泄露。

对于数字调制信号而言，载波泄露是一种带内干扰，如果载波分量较强，将直接影响整个系统的通信质量。因此，要尽量降低载波泄露。通常在基带侧微调 I Offset 或者 Q Offset 来改善载波抑制特性，这相当于引入 DC 分量，如果设置的 DC 的量和极性合适，I 和 Q 两路引起的载波泄露将相互抵消，甚至可以抵消 Mixer 的 LO 泄露带来的影响。

以上介绍了 IQ 调制器的镜频抑制及载波抑制特性，这些都是 IQ 调制器固有的特性，也是性能验证测试中必测的项目。此外，IQ 调制器还有幅频响应、三阶交调等参数，这些也都是需要测试的。不同的测试项目需要不同的测试设备和测试方法，这将是后面要介绍的内容……

[转载]数字调制系列：IQ 调制及解调简述

前面在“数字调制系列：IQ 基本理论”一文中介绍了 IQ 的概念、常用数字调制方式及映射星座图等内容，当完成数字比特流到 IQ 坐标系的映射后，便可以得到数字 I 和 Q 信号，然后分别经过 DAC 变换为模拟 I 和 Q 信号，最后经过 IQ 调制器完成上变频，图1给出了数字调制的简要架构示意图。作为整个数字调制发射系统的关键部件，IQ 调制器完成了基带信号的频谱搬移，从而达到空口传输的条件。

什么是 IQ 调制器？IQ 调制器如何工作？接收侧如何实现信号解调？本文将给出具体介绍。

1. 什么是 IQ 调制器？图2给出了 IQ 调制器的简要示意图，通常包含四个端口：模拟 I 输入，模拟 Q 输入，LO (本振)端口以及射频输出端口。有的 IQ 调制器还支持差分模拟 I/Q 输入，因此具有更多的端口。IQ 调制器包括两个对称的支路，每个支路包含一个 Mixer (上变频)；两个 Mixer 的 LO 同源，但是要求正交，即存在90°相位差。

IQ 调制器具有三个比较关键的性能指标：(1) 整个带宽内的频率响应；(2) 两个支路间的幅频响应对称性；(3) 两路 LO 信号的正交性。

这些指标的优劣将直接影响信号调制质量的好坏。IQ 调制器的频率响应包括幅频响应和相频响应，对于理想的线性时不变系统 (LTI)，幅频响应是平坦的，相频响应是线性的，信号可以无失真的传输。因此，频响性能越好，调制质量越高，从系统的角度讲，BER 越低。

为什么要强调 IQ 调制器两个支路间的幅频对称性呢？如果两个支路的频谱响应不同，就会造成 IQ 不平衡传输，当产生中心频率与 IQ 调制器 LO 频率不同的信号时，镜频分量抑制效果会变差 。因此，需要控制 IQ 调制器支路间的幅频特性差异。

类似地，两个 Mixer 的 LO 正交性也将会影响镜频抑制能力。如果完全正交，则不会对镜频抑制能力有影响。当偏离正交时，镜频分量会增强。

如果模拟 IQ 调制器的特性不是很理想，势必会影响信号的调制质量。但是，可以通过源端预失真来补偿，从而改善信号质量，比如矢量信号源中允许调整 I/Q Imbalance 及 I/Q Quadrature 参数等。

2. 发射端 IQ 调制器是如何实现上变频的？接收端 IQ 解调器又是如何实现信号解调的？此处信号的调制与解调，仅限于模拟 IQ 信号到 RF，再从 RF 信号解调出模拟 IQ 信号。通过下面的介绍，除了调制与解调的过程，您还将会了解为什么基带 I 和 Q 信号的带宽经过 IQ 调制器后会翻倍。

首先介绍一下信号的单边带频谱与双边带频谱。这两种频谱都可准确描述信号频谱，但是出发点不同，应用场景也不同。

任何一个周期信号，只要满足狄里赫利条件，均可以写为一组完备正交集函数的无穷级数。通常完备的正交集函数为三角函数，比如 {  ，  为任意非负整数}；根据欧拉公式，三角函数与虚指数函数存在一定的关系，因此周期信号也可以写为虚指数函数的无穷级数。

如果按照三角函数级数展开，则对应的频谱为单边带频谱，如果按照虚指数函数级数展开，则对应的频谱是关于零频左右对称的频谱，此时称为双边带频谱。由于运算更加方便，双边带频谱应用更加广泛。

对于调制应用而言，涉及到频谱的搬移，因此采用双边带频谱更加方便。下文所涉及的频谱，均指双边带频谱。双边带频谱包括负频率成分，没有具体物理意义，但是从数学角度讲，这些又是构成傅里叶变换的必不可少的组成部分。

图2所示的 IQ 调制器，在上变频的过程中，两个 Mixer 实际上起到乘法器的作用，即  与  相乘，  与  相乘，最后合为一路输出。

假设  和  分别为  和  的傅里叶变换，而三角函数的傅里叶变换为

根据频域卷积定理可得：

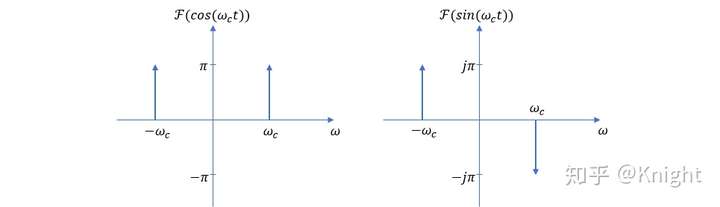
由此可见， 和  经过混频器后，从傅里叶的角度看，其双边带频谱发生了搬移，中心频率由 DC 搬移至  。傅里叶变换的产物中还包含  频率成分，如前所述，负频率不具有实际物理意义，但是作为傅里叶变换的重要组成部分，构成了整个变换的数学完整性。

虚数  的存在表明，两部分信号之间的载波存在90°相差，二者保持正交。

以上数学推导也可以由图解完成，图3给出了正余弦函数的傅里叶变换示意图，模拟 IQ 信号经过调制器后，频谱变换示意图如图4所示。

因采用双边带频谱描述信号，  和  实际带宽为双边带频谱带宽的一半，由上述推导可知，当经过IQ调制器上变频之后，整个双边带频谱搬移至射频，故输出的信号  的带宽相对于基带模拟IQ信号的带宽翻倍了。

在接收侧，射频调制信号可经过模拟IQ解调器解调，经过低通滤波器之后分别得到模拟 I 和 Q 信号。数学推导与IQ调制类似，此处不再赘述。图5给出了IQ解调器的整个图解过程，非常清晰地表明了如何由射频信号得到模拟IQ信号。

3. IQ调制与解调的实现方法有哪些？前面介绍调制及解调过程时，默认是按照模拟 IQ 调制器和解调器介绍的。现实中绝大多数数字调制发射系统均是采用了模拟 IQ 调制器，从测试设备的角度讲，矢量信号源也是采用了模拟 IQ 调制器的架构。尽管如此，IQ 调制功能也是可以通过数字的方式实现的，称为数字IQ调制器，在数字侧完成符号映射及 IQ 调制，从而得到具有载波的波形，最后经过 DAC 直接播放出来。任意波信号发生器(AWG)产生数字调制信号就是采用这种方式，但是DAC的时钟频率决定了能够输出的最高信号频率。

类似地，模拟 IQ 解调器的功能也可以由数字方式实现，称为数字下变频。而且相对于模拟解调器而言，数字下变频应用更加广泛。其基本思路为：射频信号经过下变频至 IF 频段，然后经过 ADC 直接离散化，对离散的数据作数字下变频便可以得到数字 IQ 信号，最后对 IQ 数据进一步分析。现在的矢量信号分析仪基本都是采用这个架构，有的矢量分析方案采用示波器及分析软件的方案，也是应用了数字下变频技术，如图6所示。

以上介绍了 IQ 调制器的概念、IQ 调制及解调过程及其实现方法，后面的内容将重点介绍 IQ 调制器的特性，比如镜频抑制特性、载波抑制能力，以及相对于普通上变频器，IQ 调制器的优势等。

[转载]数字调制系列：IQ基本理论

数字IQ调制凭借高数据速率以及易于实现等优势，广泛应用于无线通信系统。与传统的模拟调制不同，数字调制采用了新颖的IQ调制架构，以0、1比特流为调制信号。简单地讲，数字调制的过程就是将原始数据比特流按照一定的规则映射至IQ坐标系的过程。映射完成后将得到数字I和Q信号，再分别由DAC转换为模拟I和Q信号，最后经IQ调制器上变频至射频频段。

起初接触数字调制的时候，不知道如何理解IQ信号，疑惑比较多。经过长时间的实践和思考，略有心得体会，整理下来供大家参考。由于涉及的内容较多，本文主要介绍数字IQ调制的基本理论。

什么是IQ ？回答这个问题不得不提图1所示的矢量坐标系，横轴为实部，纵轴为虚部。数字IQ调制完成了符号到矢量坐标系的映射，映射点一般称为星座点，具有实部和虚部。从矢量角度讲，实部与虚部是正交的关系，通常称实部为In-phase分量，则虚部为Quadrature分量 。这就是IQ的由来，该矢量坐标系也可以称为IQ坐标系。

在IQ坐标系中，任何一点都确定了一个矢量，可以写为(  )的形式，数字调制完成后便可以得到相应的 I 和 Q 波形，因此数字调制又称为矢量调制。

无论是模拟调制，还是数字调制，都是采用调制信号去控制载波信号的三要素：幅度、频率和相位，分别称为调幅、调频和调相。模拟调制称为AM、FM和PM，而数字调制称为ASK、FSK和PSK。数字调制中还有一种调制方式同时包含幅度和相位调制，称为QAM调制(正交幅度调制)。下面将逐一进行介绍。

1. ASK(Amplitude Shift Keying)称为幅移键控，通常指二进制幅移键控2ASK，只对载波作幅度调制，因此符号映射至IQ坐标系后只有 I 分量，而且只有两个状态——幅度A1和A2，如图2所示。一个bit就可以表征两个状态，“0”对应A1，“1”对应A2。即一个状态只包含1 bit信息，故符号速率与比特率相同。类似于模拟AM调制，ASK也具有调制深度的概念，调制深度定义为

100%

当2ASK的调制深度为100%时，只有比特“1”有信号，比特“0”没有信号，所以称为On-Off Keying，简称为OOK调制。OOK是一种特殊的ASK调制，调制后的波形为射频脉冲信号。

图3给出了当调制源为pattern “1001110001101”时，OOK调制之后产生的波形。其中上半图为采用Rectangular filter对应的波形，脉冲波形很完美；下半图为采用Raised Cosine filter时的波形，由于该滤波器具有陡峭的滚降特性，抑制了脉冲信号的高频边带，所以脉冲波形的边沿变得很缓。因此，如果采用OOK方式产生射频脉冲串，一定要采用Rectangular filter。

2. FSK(Frequency Shift Keying)称为频移键控，常见的FSK包括2FSK、4FSK、8FSK、16FSK等。FSK一般不提及星座图，而是将符号映射至频率轴，图4以2FSK和4FSK为例，给出了经典的符号映射关系，纵轴为基带信号频率相对于FSK Peak Deviation的归一化值。

FSK是如何实现的呢？以4FSK为例，具有{-1, -1/3, 1/3, 1}四个归一化频率状态，假设FSK Peak Dev.为3MHz，则四个基带频率分别为{-3MHz, -1MHz, 1MHz, 3MHz }。选择调制源为pattern ‘00011011’，并设置符号速率为1M Sym./s，则在四个频点上都将分别持续1us，即每个符号周期内对应的都是一个CW信号。

虽然FSK并不是将符号直接映射至IQ坐标系中，但是FSK调制依然具有 I 分量和 Q 分量。因为任何一个频率不为0的基带信号，在IQ坐标系上的矢量轨迹都是一个圆，这意味着在不同时刻，该信号的 I 分量和 Q 分量也是变化的。

假设基带信号频率为  ，则用虚指数形式可以表示为  ，因此在IQ坐标系上，随着时间变化的矢量轨迹为一个圆。根据欧拉公式可得

故  。

图6给出了上述例子中4FSK调制的 I 和 Q 波形，因为符号周期为1us，所以对于  和  ，一个符号周期内包含三个周期波形。类似地，对于  和  ，包含一个周期波形。从IQ坐标系的角度看，FSK调制的过程就是沿着轨迹圆作圆周运动的过程，只是基带频率越高，运动速度越快。圆周运动过程中，改变的是载波的相位，因此也可以理解为FSK是通过调相间接实现的。

如果符号速率较高，则符号周期较短，FSK调制过程中很有可能出现一个符号周期只包含部分波形的情况，如图7所示，除了+/-3MHz两个频点是一个完整的周期，+/-1MHz两个频点只有部分波形。

3. PSK(Phase Shift Keying)称为相移键控，是非常主流的数字调制方式，常用的PSK包括BPSK、QPSK、OQPSK、8PSK等。PSK调制是将符号直接映射到IQ坐标系上的，图8给出了几组常用的映射方式。

下面以QPSK为例，介绍符号映射的过程，其它PSK调制过程与此类似。假设比特流为“00 01 11 10 01 00 11 10 00 11”共10个符号，按照图8的映射方式，可以得到图9所示的IQ基带波形及其矢量轨迹图。

图中数字1~9表示符号点的跳变轨迹，比如跳频路径1是指从符号(00)跳变至(01)的矢量轨迹，跳频路径2是从符号(01)跳变至(11)的矢量轨迹。其中跳频路径4、6和9会出现 I 和 Q 同时为0的情况，意味着这一瞬间将没有信号输出。这将导致输出的射频信号具有较高峰均比PAR，如果要求发射平均功率达到某一水平，高PAR对应的峰值功率将更高，对功率放大器的设计提出了挑战。

为了规避这种过零点“行为”，通过将Q路信号延迟半个符号周期，此时 I 和 Q 不会同时为0，符号跳变时也就绕开了原点，如下图所示。这种QPSK调制一般称为Offset QPSK，简称为OQPSK；有的文献称为staggered QPSK，简称为SQPSK。

4. QAM(Quadrature Amplitude Modulation)称为正交幅度调制，属于高阶数字调制，一个符号携带多个bit信息，比如16/32/64/128/256/512/1024 QAM等，因此在移动通信中较为常用。前面介绍的PSK调制并不会改变载波的振幅，只是改变其相位，而QAM调制相当于调幅和调相结合的调制方式，不仅会改变载波振幅，还会改变其相位。

图11以16QAM调制为例，给出了常用的映射星座图，具有16个星座点，因此一个符号携带4 bits信息。16QAM调制的 I 和 Q 路信号为4电平信号，作为示例，图12给出了pattern为“0100 0101 0011 1100 0000 0010 1001 1100”对应的16QAM调制的基带IQ信号波形。

IQ坐标系上映射星座点的 I 和 Q 决定了载波信号的振幅，而不是包络。为了便于证明，下面使用IQ调制的方式产生一个与载波同频的CW信号，对应的 I 和 Q 分量为一个常数，假设取图1所示的映射点，  ，  。经过图13所示的IQ调制器上变频后得到射频信号  为

可见，射频信号是振幅为1的连续波信号，因此  定义了载波信号的振幅。

根据16QAM的星座图可知，任意两个符号之间都有可能存在跳变，而每个符号映射点对应的矢量模值可能不同，相位也可能不同，因此QAM调制会导致载波的振幅发生变化，同时相位也发生变化。

以上简单介绍了常见的几种通用数字调制方式，有时由于系统需要，要求的调制方式比较特殊，这种情况下可以自定义数字调制。自定义数字调制其实就是根据要求自定义星座图，然后按照映射规则实现符号映射，从而完成调制。通常标准测试设备AWG或者VSG都允许用户自定义数字调制，并提供相应的操作界面，图14是Tek一款AWG自定义数字调制的界面，可以直接调整IQ坐标。

对于PSK和QAM调制，为了限制信号带宽，防止ISI，一般都会采用Pulse Shaping Filter对数字IQ信号进行滤波。关于Pulse Shaping Filter将在后面介绍基带IQ信号带宽与射频带宽之间的关系时作介绍。